Straight Line Depreciation
Verink has developed a
generalized equation that is particularly adapted to corrosion engineering
problems. This equation takes into account the influence of taxes, straight-line
depreciation, operating expenses, and salvage value in the calculation of
present worth and annual cost. Using this equation, a problem can be solved
merely by entering data into the equation with the assistance of compound
interest data: (reference)
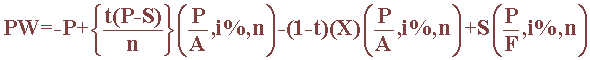
- where:
- A represents the annual end-of-period cash flow
- F represents a future sum of money
- i% represents the interest rate
expressed as a decimal
- n is the number of years
- PW is the present worth referred also as Net Present Value (NPV)
- P is the cost of the system at time 0
- S represents salvage value
- t is the tax rate expressed as a decimal
- X represents the operating expenses
- First Term [-P]: This term
represents the initial project expense, at time zero. As an expense, it is
assigned a negative value. There is no need to translate this value to a
future value in time, as the PW approach discounts all money values to the
present (time zero).
- Second Term [{t(P-S)/n}(P/A,
i%, n)]: the second term in this equation describes the
depreciation of a system. The portion enclosed in braces expresses the
annual amount of tax credit permitted by this method of straight-line
depreciation. The portion in parentheses translates these as equal amounts
back to time zero by converting them to present worth.
- Third Term [-(1-t)(X)(P/A,
i%, n)]: the third term in the generalized equation
consists of two terms. One is (X)(P/A, i%, n) that represents the cost of
items properly chargeable as expenses, such as the cost of maintenance,
insurance, and the cost of inhibitors. Because this term involves
expenditure of money, it also comes with a negative sign. The second part,
t(X)(P/A, i%, n), accounts for the tax credit associated with this business
expense and because it represents a saving it is associated with a positive
sign.
- Fourth Term [S(P/F,
i%, n)]: the fourth term translates the future value of
salvage to present value. This is a one time event rather than a uniform
series and therefore it involves the single payment present worth factors.
Many corrosion measures, such as coatings and other repetitive maintenance
measures, have no salvage value, in which cases this term is zero.
Present Worth (PW) can be converted to equivalent annual cost (A) by using
the following formula: