Module Four of CCE 281 Corrosion: Impact, Principles, and Practical Solutions

Nernst Equation

The Nernst equation was named after the German chemist Walther Nernst who established very useful relations between the energy or potential of a cell to the concentrations of participating ions. This equation can be derived from the equation linking free energy changes to the reaction quotient (Q_reaction): (reference)

where, for a generalized equation of the form:

The capital letters A, B, M and N in equation represent respectively the reactants and products of a given reaction while the small letters represent the coefficients required to balance the reaction.

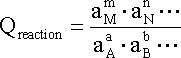
At equilibrium, DG = 0 and Q_reaction corresponds to the equilibrium constant (K_eq) described earlier.

In the case of an electrochemical reaction, substitution of the relationships DG = -nFE and DG⁰ = -nFE⁰ into the expression of a reaction free energy and division of both sides by -nF gives the Nernst equation for an electrode reaction:

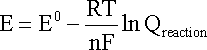
Combining constants at 25^oC (298.15 K) gives the simpler form of the Nernst equation for an electrode reaction at this standard temperature:

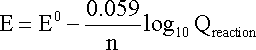
In this equation, the electrode potential (E) would be the actual potential difference across a cell containing this electrode as a half-cell and a standard hydrogen electrode as the other half-cell. Alternatively, the relationship in equation can be used to combine two Nernst equations corresponding to two half-cell reactions into the Nernst equation for a cell reaction:

Some of the species that take part these electrode reactions are pure solid compounds and pure liquid compounds. In dilute aqueous solutions, water can be treated as a pure liquid. For pure solid compounds or pure liquid compounds, activities are constant and their values are considered to be unity. The activities of gases are usually taken as their partial pressures and the activities (a_i) of solutes such as ions are the product of the molar concentration and the activity coefficient of each chemical species (i):

The activity coefficient (g_i) in equation can be a complex function highly dependent on a multitude of variables often difficult to even estimate. For this reason it is usually convenient to ignore (g_i) and use the concentration term [i] as an approximation of a_i.